Many types of professionals analyze data using different skills. Microsoft Excel users analyze data using Excel PivotTables, while data scientists use statistical and machine learning models. 

Despite this diversity, Excel users, data scientists, and statisticians share one universal data analysis skill: visually analyzing data.

This is the first in a five-part blog series introducing you to visually analyzing data with Python in Microsoft Excel.

By the end of the blog series, you will have built fundamental skills in visually analyzing numeric, categorical, and time-series data. These skills are valuable to any professional, regardless of role or industry.

Each post in the series has an accompanying Microsoft Excel workbook to download and use to build your skills. This post’s workbook is available for download here.

For convenience, here are the links to all the blog posts in this series:

• Part 1 – Using Histograms (this post)
• Part 2 – Using Box Plots
• Part 3 – Using Scatter Plots
• Part 4 – Using Bar Charts
• Part 5 – Using Line Charts

There are a few things to note about this blog series: 

• First, if you are new to Python in Excel, you should start with my Python for Excel Analysts blog series as it covers many concepts that are assumed in this blog series.

• Second, this series assumes you have enabled the Python in Excel public preview. This Microsoft article provides you with the information needed to get access to Python in Excel.

• Third, the blog series will use the Microsoft Excel Labs Python Editor for writing code. However, this Python Editor is not required. All code can be entered using the Formula Bar and the new PY() function.

• Lastly, the blog series uses the Anaconda Toolbox for sourcing datasets. However, using the Toolbox is not necessary. All data is included in the Excel workbook downloads.

Summarizing Numeric Data

One of the most common data analysis scenarios is crafting insights from a column of numbers. These numbers could be anything – order counts, sales amounts, patient ages, etc.

If the column is small (e.g., 10 individual values), it is relatively easy to look at the raw numbers and craft insights by answering the following questions:

1. What are the minimum and maximum values?
2. How widely do the values vary?
3. What is a typical value for the collection of numbers?

However, a column is rarely so small to allow for this. As humans, our ability to craft insights about a column of numbers drops precipitously with larger columns. 

This is where summarizing a column of numbers comes into play. Microsoft Excel functions like MIN(), MAX(), STDEV.S(), and AVERAGE() are commonly used to summarize numeric data and provide insights.

While the above functions (and the Python equivalents) are undoubtedly helpful, they only tell part of the story. This is where visually analyzing columns of numbers enters the picture (pun intended!).

US State Population Data

This post will use 2014 population data for the 50 US states, the District of Columbia, and Puerto Rico to introduce you to visually analyzing columns of numbers.

NOTE – The Excel workbook accompanying this blog post has a Raw Data worksheet containing the dataset that can be used instead of importing the data using the Anaconda Toolbox.  

This dataset is easily accessible from the Anaconda Toolbox Add-in. The Toolbox lives in the Excel Ribbon under Formulas:

Fig 01 – Locating the Anaconda Toolbox

After signing into the Toolbox, you will be presented with the following:

Fig 02 – The Anaconda Toolbox User Experience

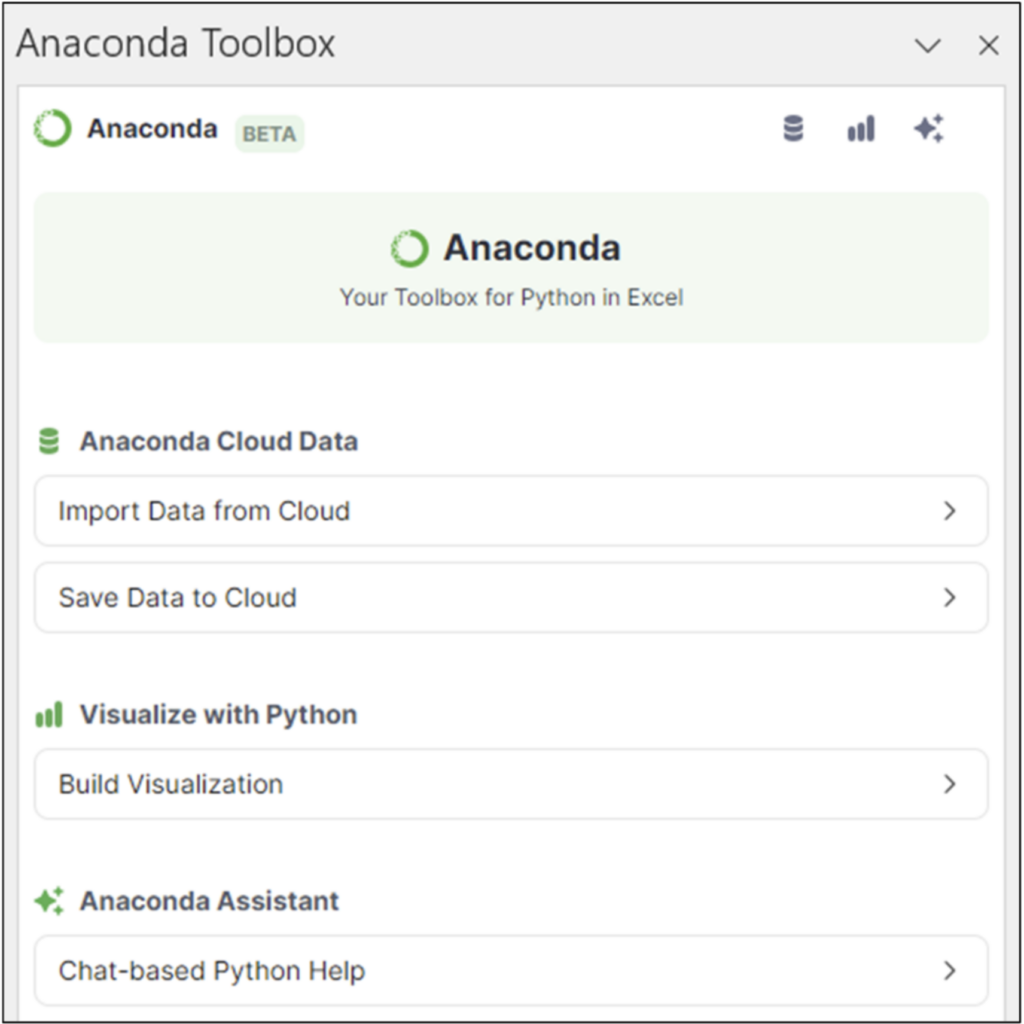
The Toolbox offers several features beyond sourcing datasets. These features will be the focus of upcoming content (e.g., blogs and courses) from Anaconda.

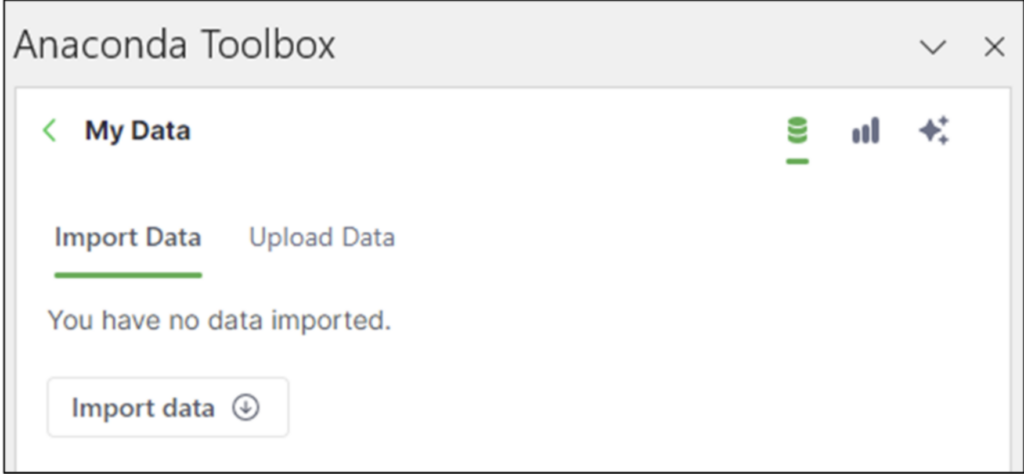
Anaconda offers many free datasets that can be imported into your Excel workbooks. Clicking Import Data from Cloud in the Toolbox displays what data you have already imported:

Fig 03 – Existing Data Imports

Clicking the Import data button provides the following options:

Fig 04 – Import Data Options

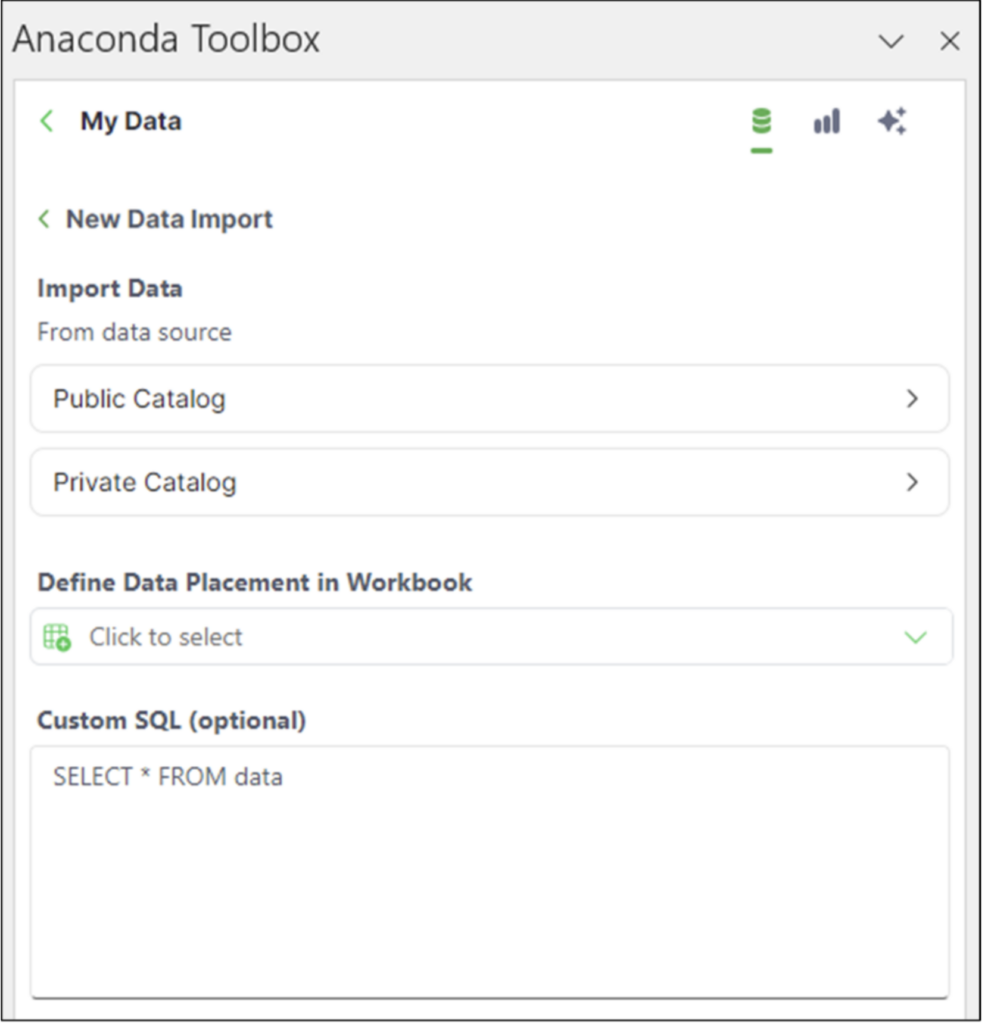
The dataset used in this blog post is in the Public Catalog. Clicking this option lists the publicly available datasets:

Fig 05 – Publicly Available Datasets

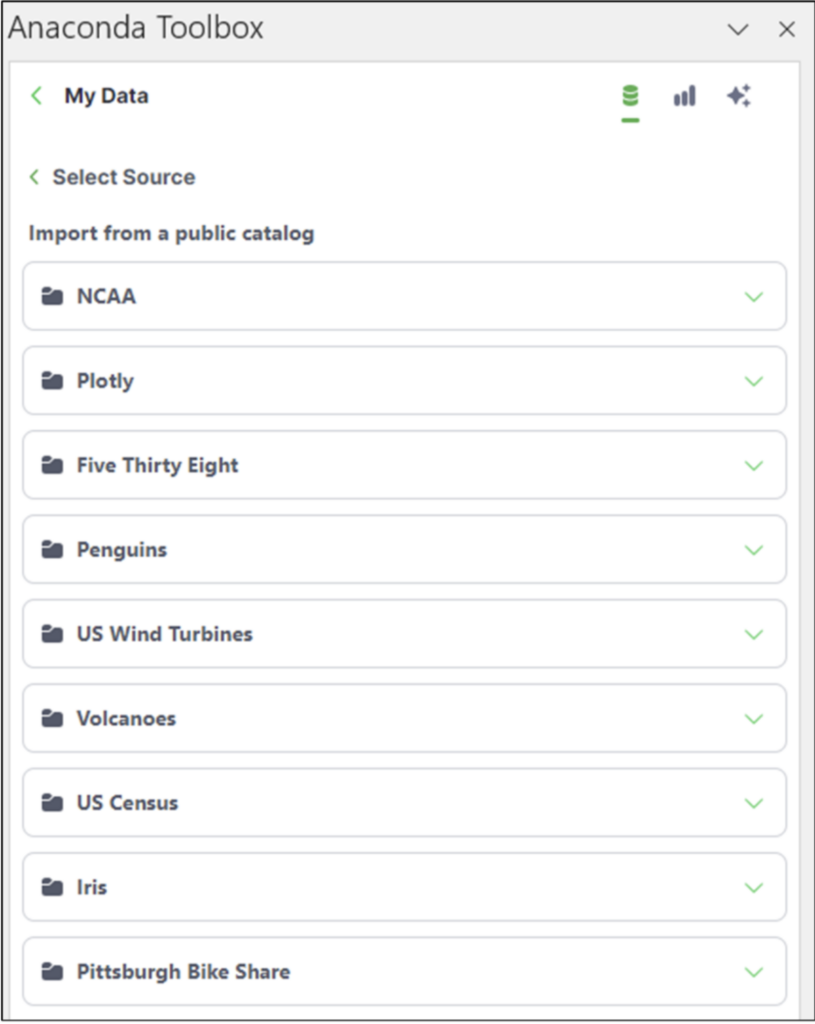
The 2014_us_states_population dataset resides within the Plotly folder. Clicking on the folder lists the Plotly datasets:

Fig 06 – The 2014_us_states_population Dataset

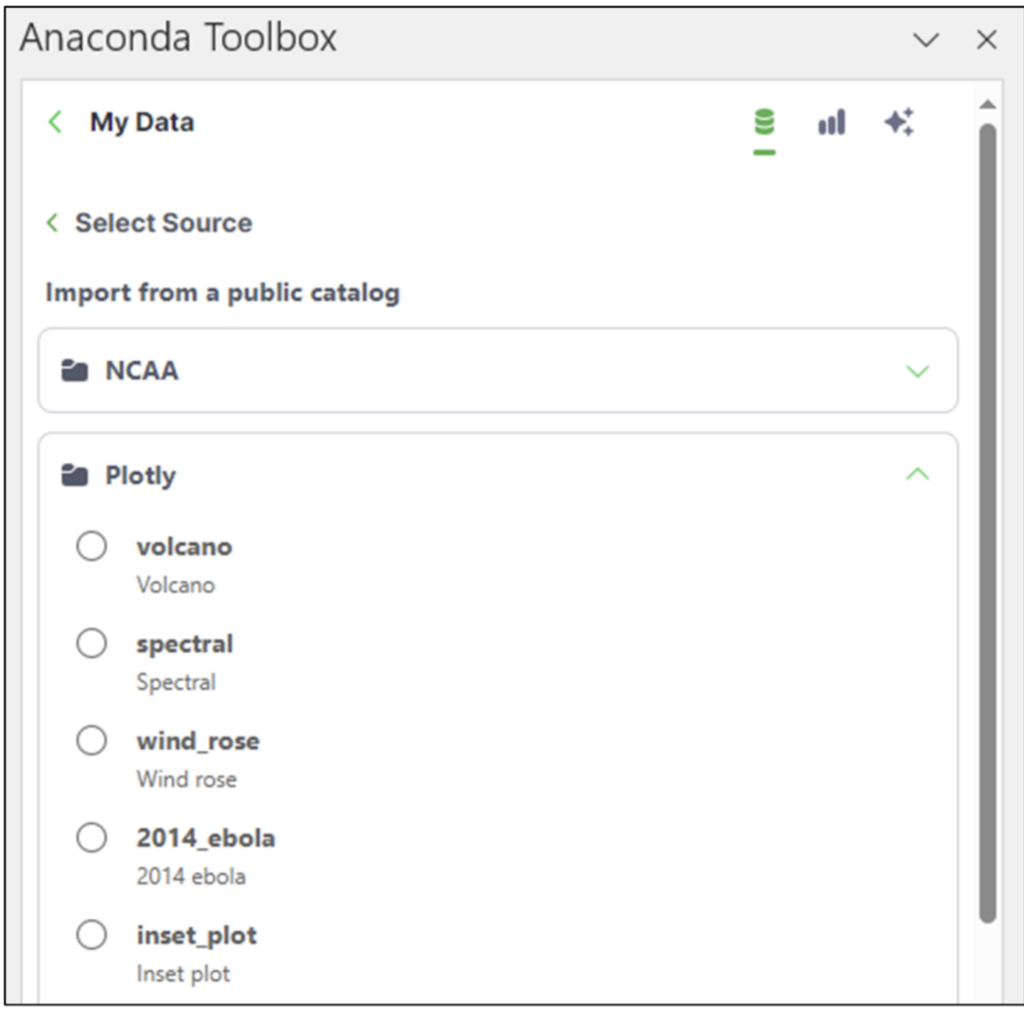
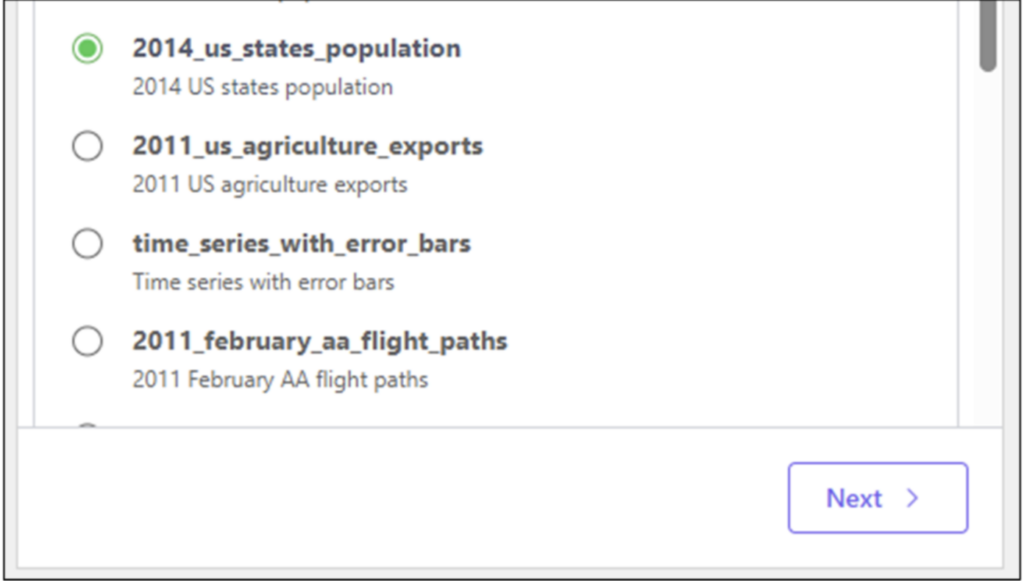
Scroll down the list to the 2014_us_states_population dataset, select it, and then click the Next button. Within the Toolbox, select the US State Pop 2014 worksheet:

Fig 07 – Select Where to Import the Data

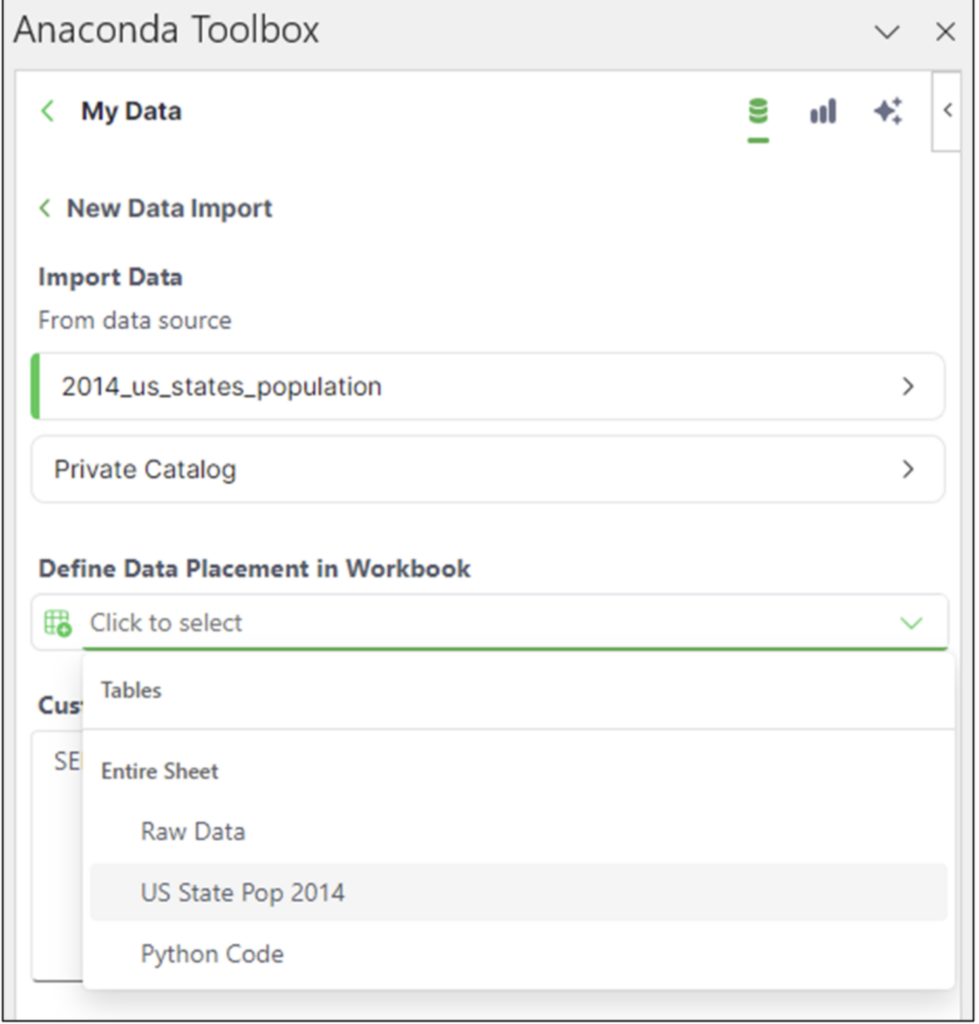
With the worksheet selected, click the Import button. The data will be loaded into the selected worksheet:

Fig 08 – The Imported US State Population Data

Tallying Columns of Numbers

The average of the Population column of the dataset is approximately 6.2 million. The average is one way of calculating a typical value given a column of numbers.

While the average is certainly useful, it doesn’t provide us with a complete picture of what’s going on in the data. What we want to know is how the data is distributed. 

The following questions are related to how the data is distributed:

1. Are the values, in general, close to the average?
2. Are there many values much smaller than the average?
3. Are there many values much larger than the average?

One way to answer these questions is by tallying up the individual values. Using Excel, you can quickly accomplish the tally using a sorted PivotTable:

Fig 09 – Tallying the Population Column Values

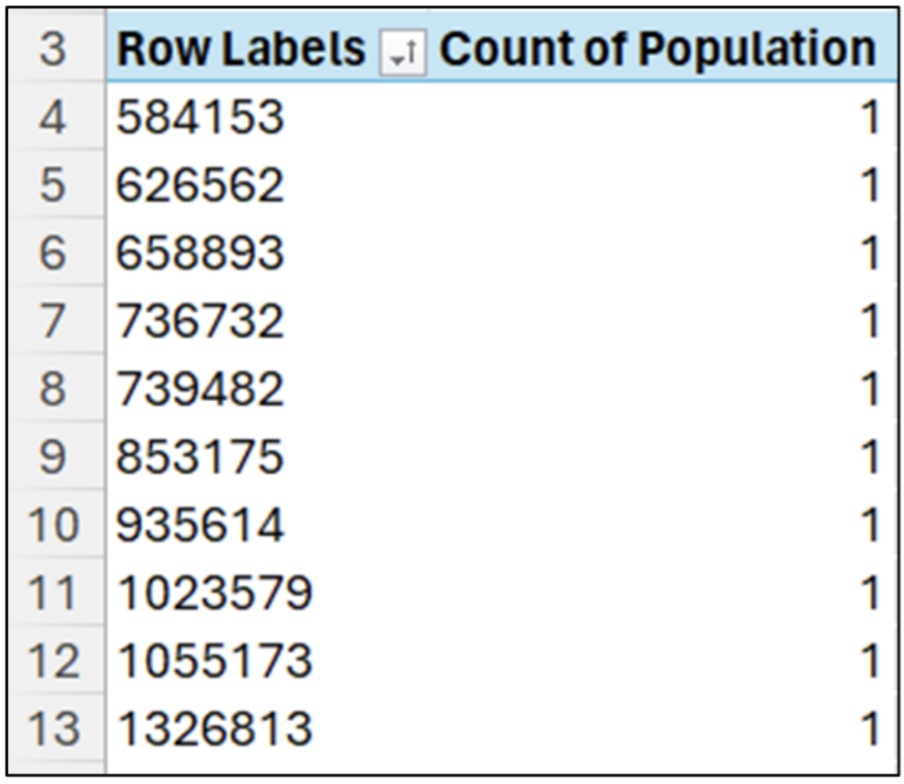
Tallying numeric data means finding how many times each unique value appears in the column. 

In the case of the Population column, every value is unique (i.e., every value appears exactly once). What we can already see in Fig 09 is that there are many values far less than 6.2 million. 

Scrolling down the tally list shows that more than half the values are less than the average (i.e., 34 out of 52 values).

Fig 10 – 34 Out of 52 Population Values Are Less Than the Average

Tallying the values in the Population column has already shown us two things:

1. The average of the Population column hides a lot about what’s going on in the data.
2. It’s common to have many unique values in a column of numbers, making tallies not very scalable.

Fixing the second thing is relatively easy.

Binning the Numbers

As the size of numeric columns increases, you typically see more unique values. Rather than tallying individual values, it is more common to use bins to define ranges of values to tally. 

What is counted is how many column values fall within each bin. Excel PivotTable groups provide a way to implement bins for a column of numbers.

Fig 11 – Binning the Population Column

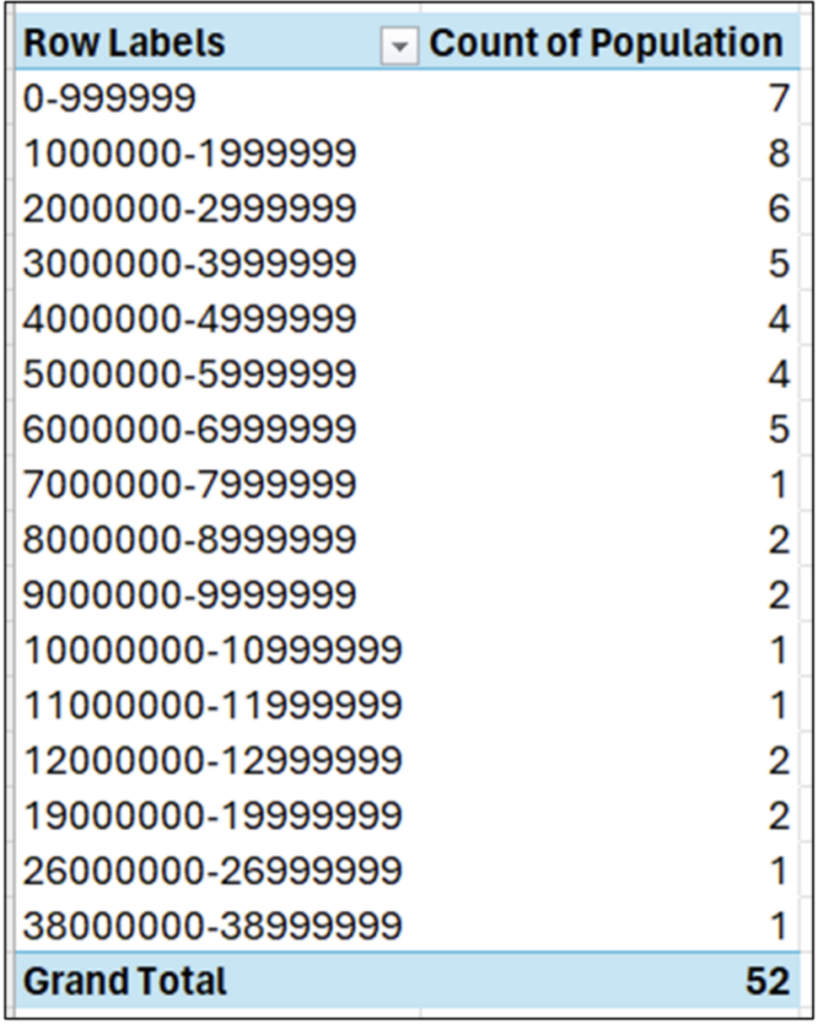
Fig 11 illustrates the power of binning. For example, we can quickly see that half the data (i.e., 26 out of 52 values) are less than 4.0 million – significantly less than the average of 6.2 million.

As useful as binning is, we’re still using a table to analyze the distribution of numbers. While tables are certainly useful, they are suboptimal for detecting data patterns.

Humans are far better at detecting patterns using visualizations.

Visualizing the Bins

A histogram visualizes binned numeric data. Histograms are the default for visually analyzing columns of numbers. If you’ve ever taken a statistics course, you’ve seen histograms.

Microsoft knows how valuable visual data analysis is to any professional and has made it easy for Excel users by including access to Python’s powerful data visualization libraries by default.

Within the Excel Ribbon, accessing the Formulas option allows you to see which Python libraries are included by default.

Fig 12 – View Which Python Libraries Are Included by Default

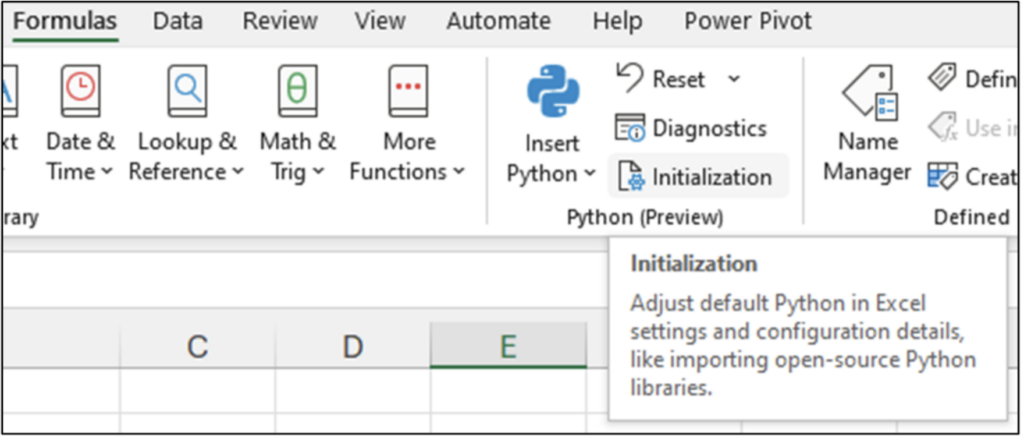
The Python Preview Initialization option displays a number of libraries:

Fig 13 – The Default Python Libraries

In this blog series, we will use the seaborn and matplotlib.pyplot libraries for data visualization.

Your First Histogram

The seaborn library has become a go-to for Python data visualizations due to ease of use. 

Using seaborn, you can quickly create powerful data visualizations that are difficult or impossible to create using out-of-the-box Excel.

While Microsoft Excel supports creating histograms, the functionality is limited. Additionally, using seaborn is often faster than using the Excel GUI interface.

The first step is to open the Excel Labs Python Editor from Excel’s Home Ribbon:

Fig 14 – Accessing the Excel Labs Python Editor

NOTE – All code can be entered in the Formula Bar via the PY() function if you don’t have the Python Editor.

We’ll use the Python Code worksheet for writing code in this blog post because it offers a richer coding experience than using the traditional Excel Formula Bar.

Fig 15 – Using the Python Code Worksheet for Coding

In the Excel Labs Add-in, clicking Add Python cell in B1 opens the Python Editor. Entering the following code loads the US state population dataset as a pandas DataFrame:

Fig 16 – Loading the US State Population Data

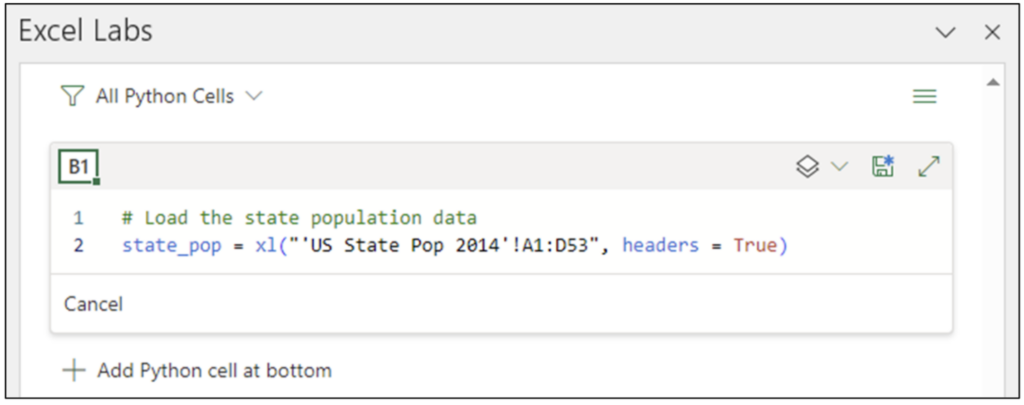
NOTE – Be sure to change the code above if you’re using the Raw Data worksheet from ‘US State Pop 2014’ to ‘Raw Data.’

Clicking the disk icon in the Python Editor will execute the code:

Fig 17 – Executing the Python Code

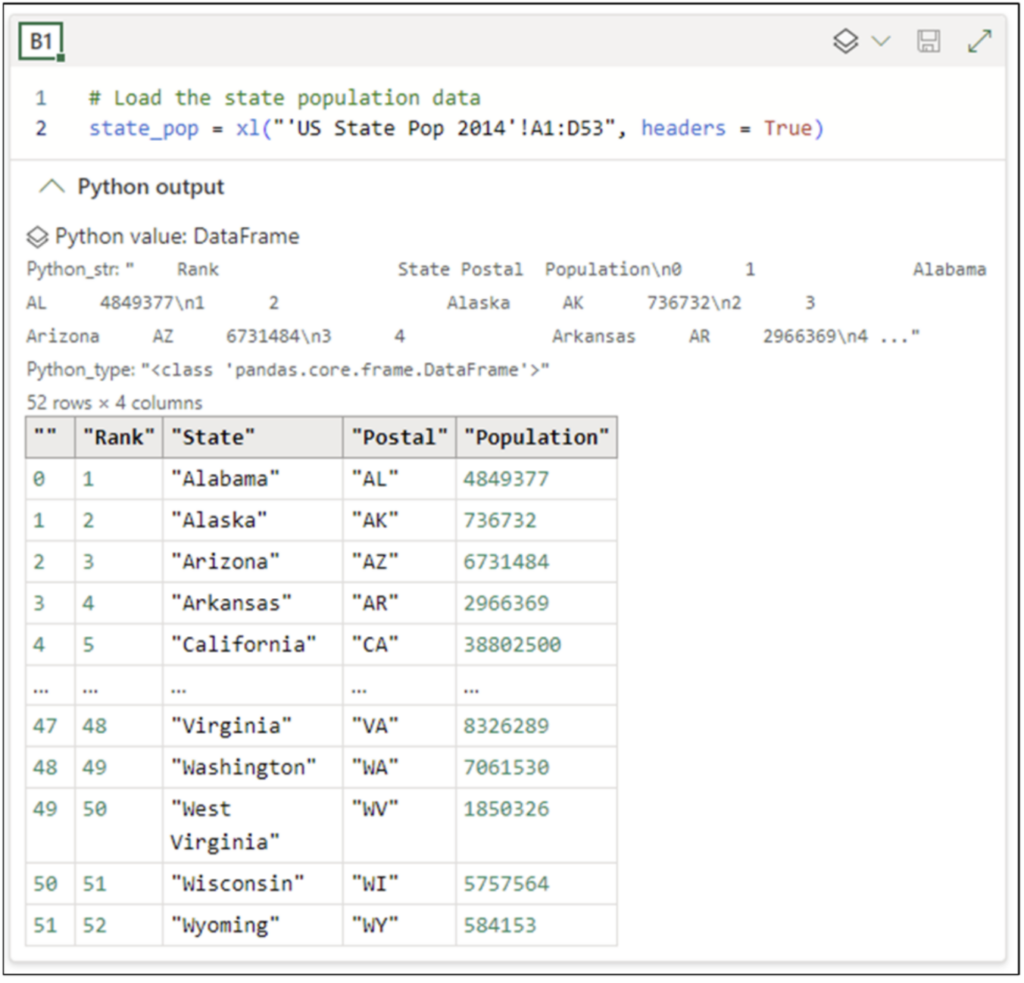
When the code has been executed, you can check the Python Editor’s Python Output to see a preview of the DataFrame:

Fig 18 – A Preview of the Loaded DataFrame

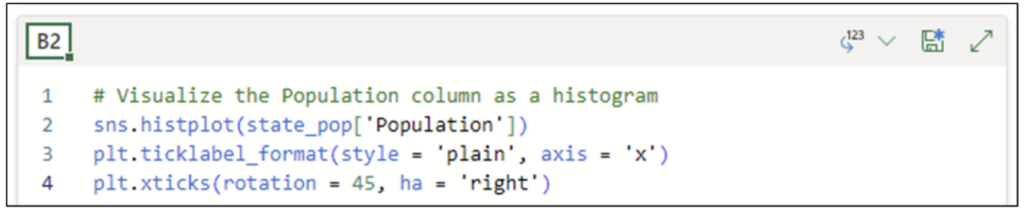
Within the Python Editor, clicking Add Python Cell at bottom will open a new Python editor window for cell B2. The following Python code demonstrates creating a histogram of the Population column:

Fig 19 – Python Code for Creating a Histogram

The code above uses the histplot() function from the seaborn library. The function is accessed using the sns alias that Microsoft provides by default.

Before running the Python code in cell B2, the output should be changed to Convert to Excel values by clicking the downward arrow: 

Fig 20 – Changing Python Cell Output to Excel Values

Executing the Python code in cell B2 produces a histogram within the cell. Expanding the size of the cell allows you to clearly see the histogram:

Fig 21 – Your First Histogram

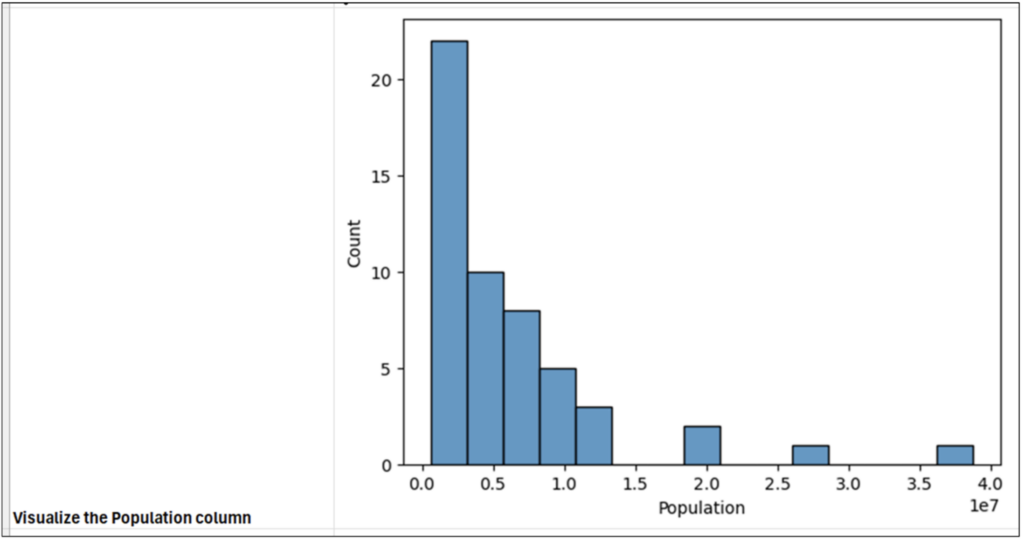
Unfortunately, the histogram produced by default using the histplot() function has several issues. So let us write some code to improve our histogram.

Improving the Histogram

While there is nothing technically wrong with the histogram depicted in Fig 21, it can be improved in the following two ways:

1. The values along the x-axis can be made easier to understand.
2. Adding a vertical line to the histogram representing the average of all the data helps the analysis.

Adding the following code to cell B2 will convert the x-axis values from scientific notation to whole numbers. The code uses the ticklabel_format() function from the pyplot library using the plt alias:

Fig 22 – Changing the X-axis to be Whole Numbers

Executing the code in B2 produces the following updated histogram:

Fig 23 – The Updated Histogram

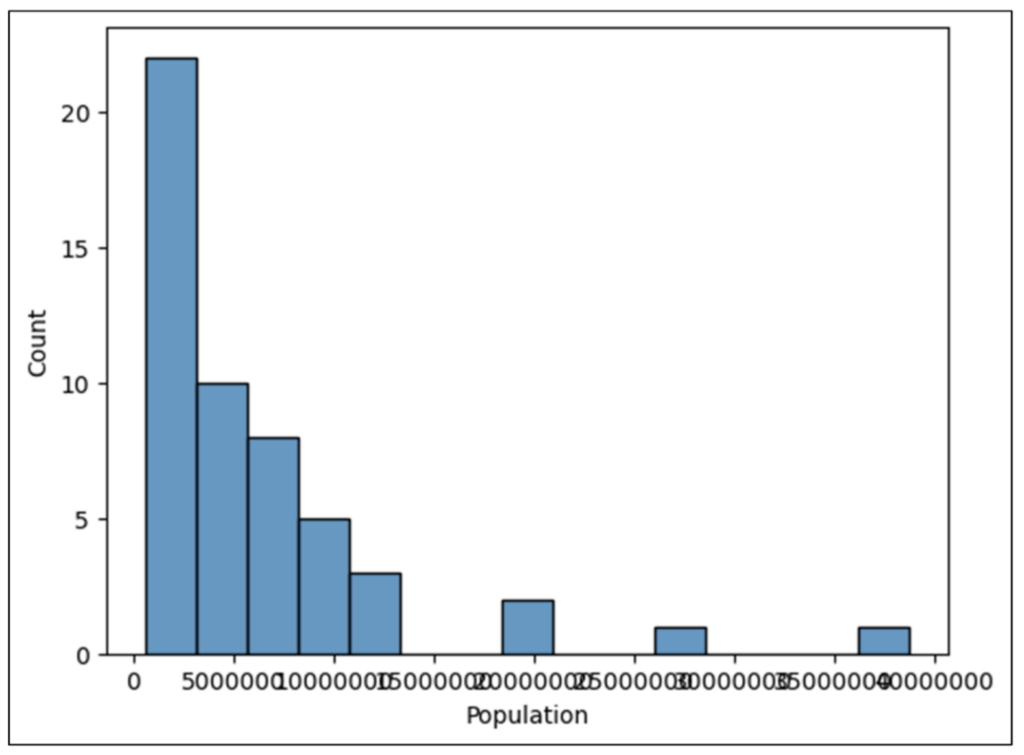
Unfortunately, the size of the whole numbers makes the x-axis impossible to read. Adding code to use the pyplot xticks() function will rotate the x-axis labels 45 degrees to the right:

Fig 24 – Code for Rotating X-axis Labels

Running the code of Fig 24 produces the following histogram:

Fig 25 – Histogram with Rotated Labels

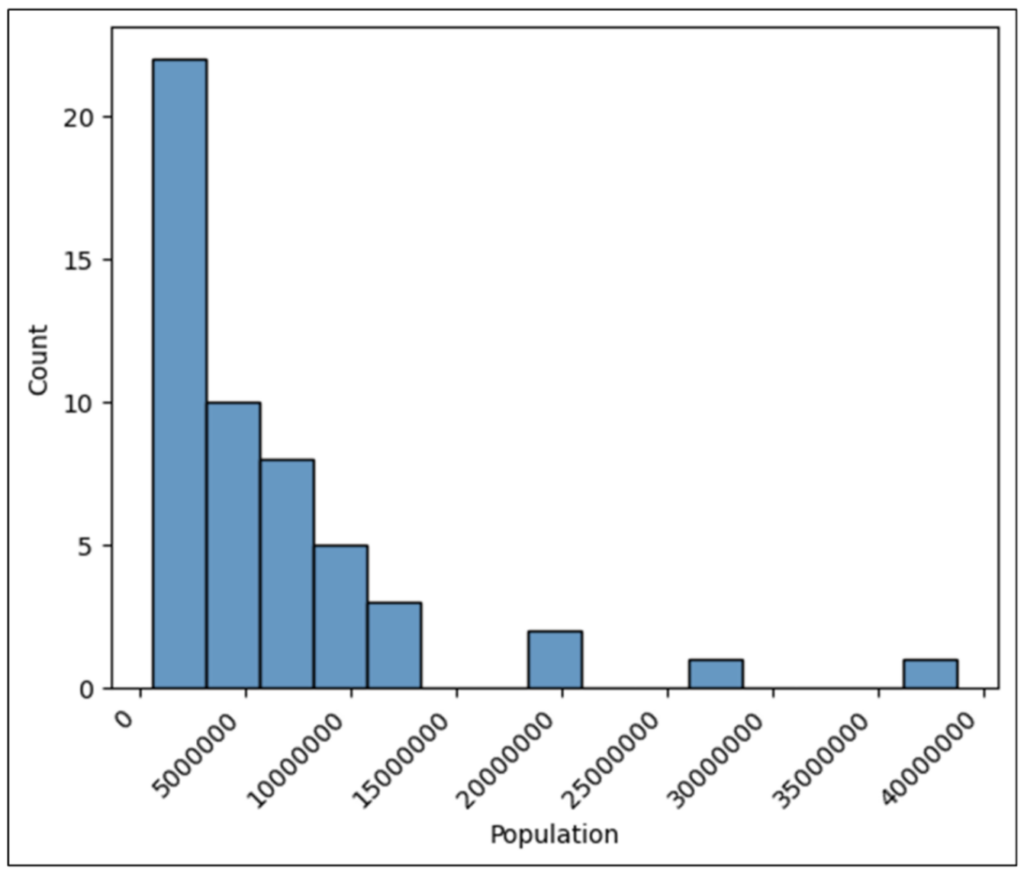
The final improvement to the histogram is to add a vertical line corresponding to the average of the Population column values. Using the pyplot axvline() function adds the line to the histogram: 

Fig 26 – Adding an Average Line to the Histogram

The code in Fig 26 uses the mean() method. This method calculates the arithmetic mean of a column of numbers. Think of the mean as just another name for calculating the average.

Executing the code of Fig 26 produces the final version of the histogram that will be used for analysis:

Fig 27 – The Final Histogram for Analysis

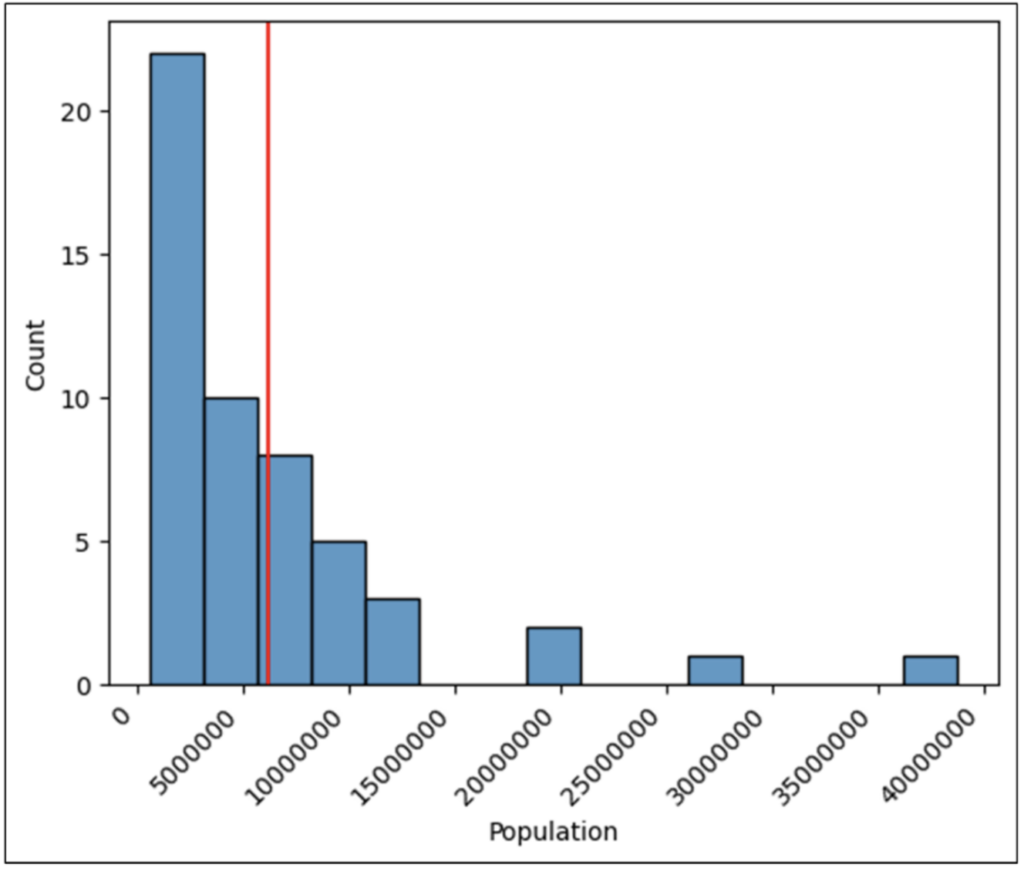
Analyzing Histograms

When analyzing histograms, you are examining the visualization to understand the following characteristics:

1. Spread
2. Center
3. Shape

The following subsections will address each of these characteristics using the final version of the histogram.

Histogram Spread

The spread of a histogram is the range of values depicted from the highest to the lowest: 

Fig 28 – The Spread of the Population Histogram 

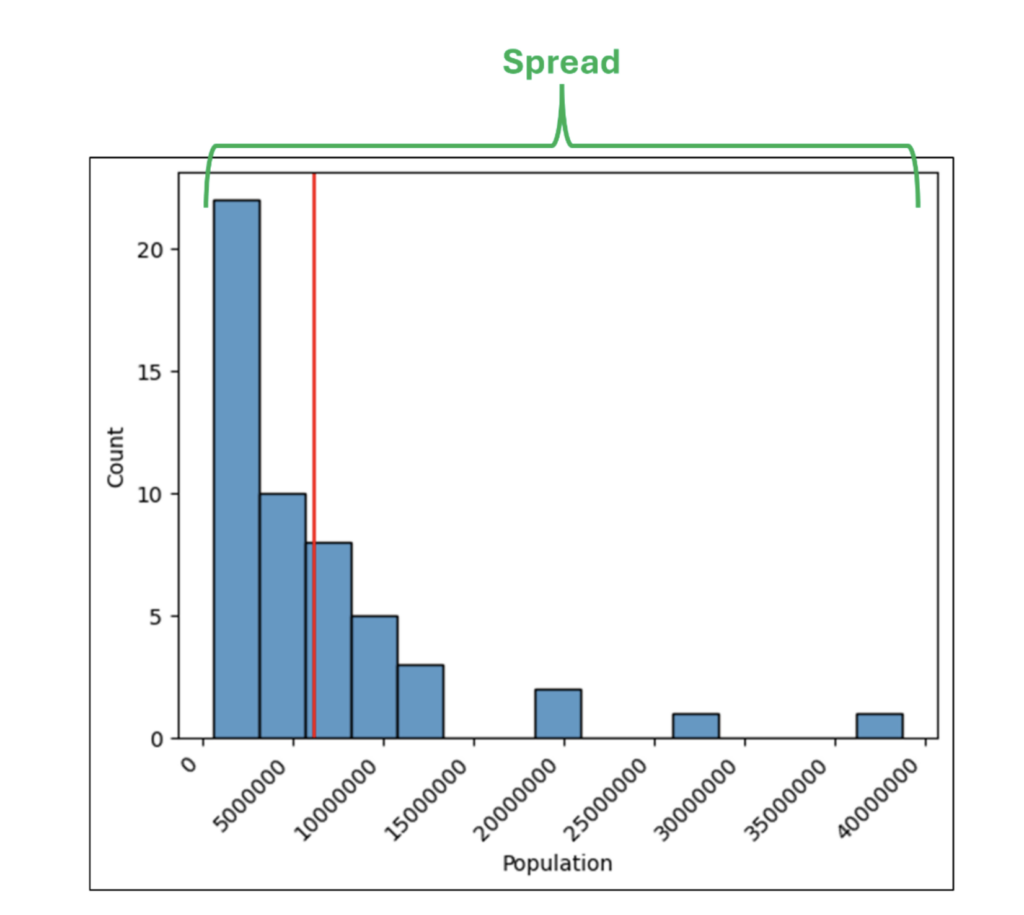
The spread of a histogram provides initial insights into the distribution of the numeric data:

1. Minimum and maximum values.
2. Areas where no values are present (i.e., gaps).

On examining the spread in Fig 28, we can see that the populations of the US states range from under 1 million up to approximately 38 million.

Examining the spread also tells us that there are few US states with populations above 15 million and that there are many gaps in the distribution (e.g., no US states have a population between 30 and 35 million).

Examining a histogram’s spread helps to answer the following questions:

1. Do minimum and maximum values make sense for the data being analyzed?
2. If there are gaps, do they make sense for the analyzed data?

Answering the above questions usually requires domain expertise/knowledge.

Histogram Center

The center of a histogram is a representation of the typical value for a collection of numeric data (e.g., a column in a DataFrame).

Statisticians refer to this idea of a typical value as a measure of location or central tendency. 

The most used measure of location is the mean (i.e., the average), although others are also used (e.g., the median):

Fig 29 – The Center of the Histogram

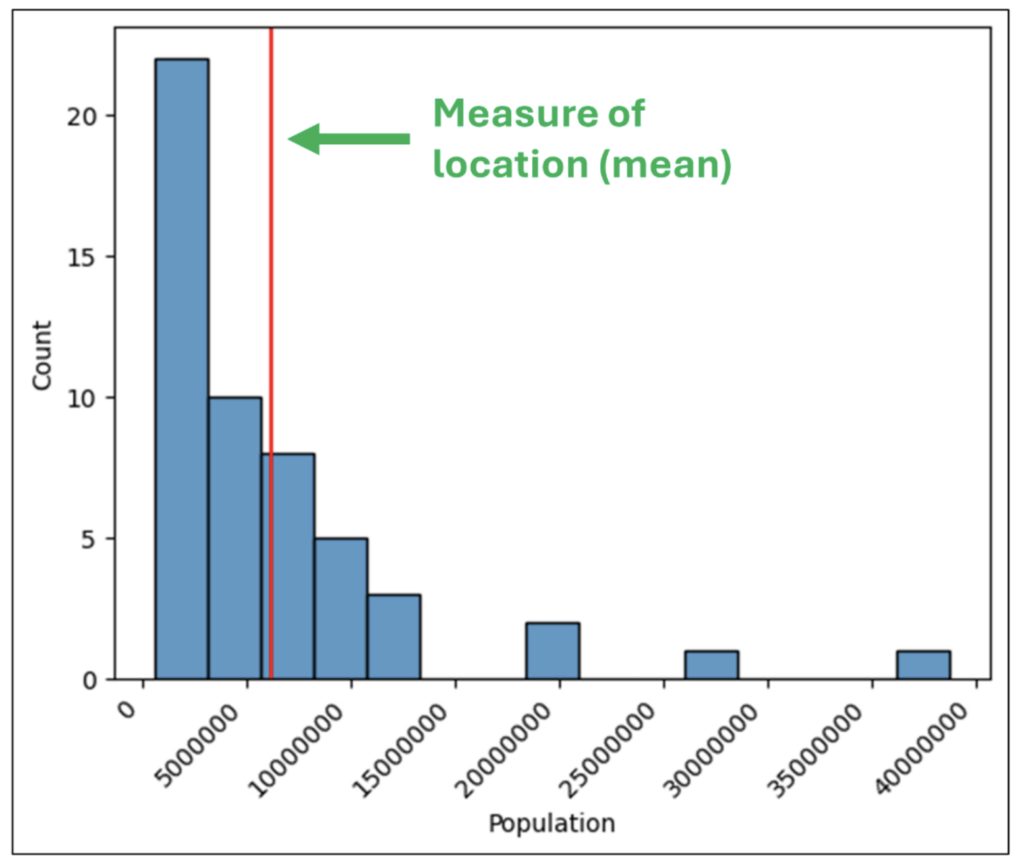
Examining the shape depicted in Fig 29 reveals that most of the values are bunched up at the left end of the histogram and are lower than the mean.

In other words, the mean isn’t representative of a typical value of the data (e.g., because some huge states like California inflate the mean).

Also, on examining the shape depicted in Fig 29, we can conclude that most US states skew to smaller populations and we need a better method to represent a typical value (e.g., the median).

Histogram Shape

The shape of a histogram is the representation of the density of values throughout the histogram’s spread.

Examining a histogram’s shape helps to answer the following questions:

1. Are many values bunched up at one end of the spread?
2. Are many values bunched up at both ends of the spread (i.e., the histogram looks like a valley)?
3. Is the histogram mound-shaped and symmetrical around the mean (i.e., is the histogram a bell curve)?
4. Are there multiple peaks?

Let us apply the above questions to the histogram.

Fig 30 – The Shape of the Histogram

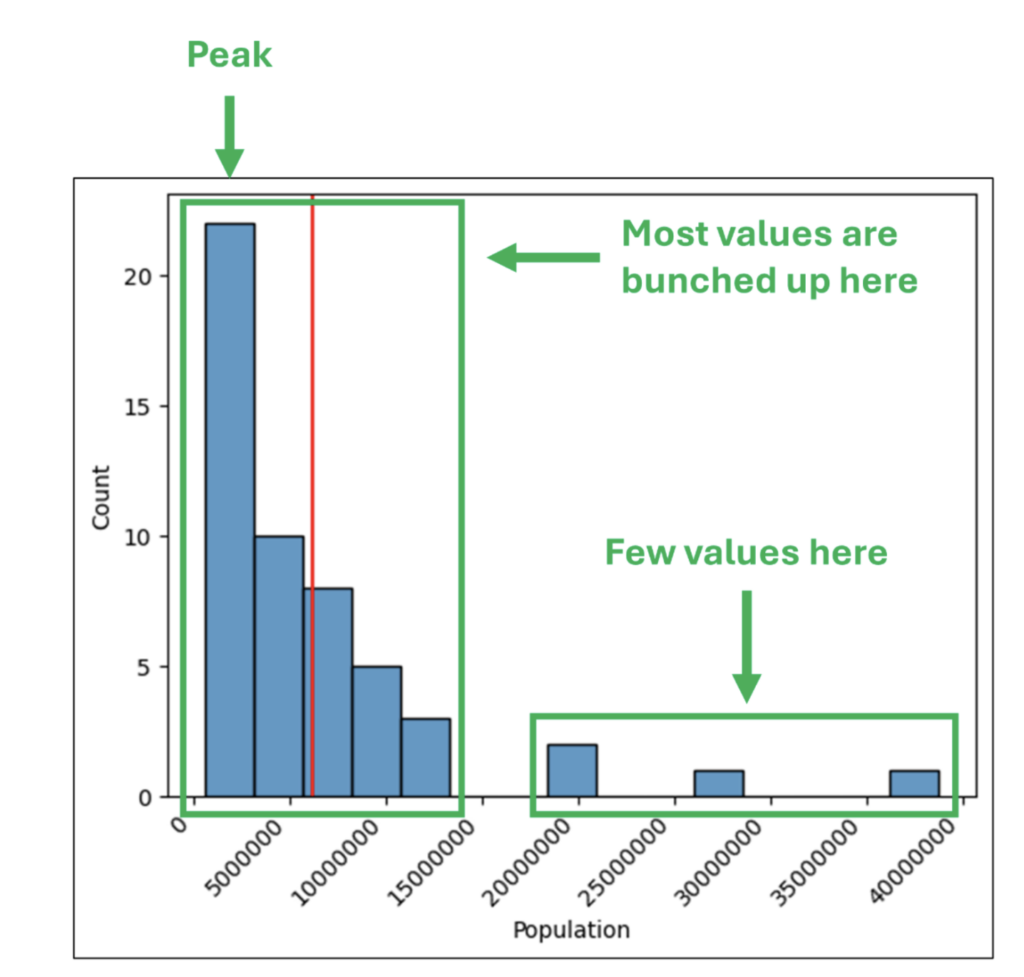
The shape depicted in Fig 30 tells the story that US state populations are mostly small, with a few states contributing disproportionately.

For example, the combination of Florida, Texas, and California represents 26.6% of the entire US population.

The shape of a histogram not only tells us a lot about the distribution of numeric values but also provides us hints for further investigations.

Considering the nature of the dataset, one potential investigation might be to evaluate whether landlocked states have predominantly smaller populations.

Changing Histogram Shapes

The shape of a histogram is primarily determined by the size of the bins used. 

Generally, decreasing the bin size leads to more bars that are typically not as tall, while increasing the bin size leads to less bars that are taller.

The binwidth parameter can be used to control the bins’ size (i.e., the width) in a histogram. The following code uses a binwidth of 1,000,000:

Fig 31 – Changing binwidth to be 1,000,000

And here is the resulting histogram:

Fig 32 – Histogram with Bins of 1,000,000

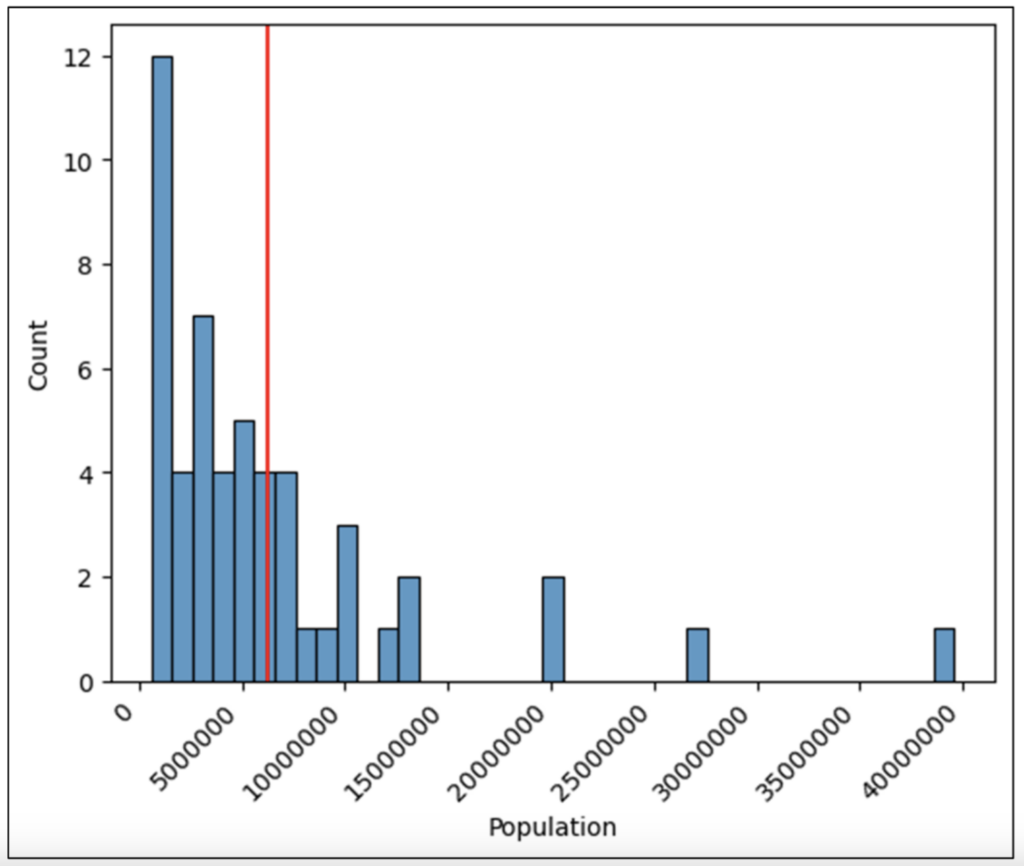
For any given dataset, there is no definitive rule on how large the bins should be. It is common to experiment with a few bin sizes based on subject matter expertise.

If you’re interested in learning some rules of thumb for determining histogram bin sizes, check out this article.

What’s Next?

Histograms are the most fundamental way to analyze numeric data visually, but they are not always the best in every situation.

Here’s an example – you would like to compare the distribution of sales order amounts by product line.

The next post in this series will teach you how to use box plots to conduct this type of analysis. If you like this blog series, check out my self-paced certification program, Anaconda Certified: Data Analysis with Python in Excel.

Until next time, stay healthy and happy data sleuthing!